| |
Scalar (标量) and Vector (矢量)
Two types of physical quantities:
· Scalar: described by a single number. Example: time, temperature, length, mass, density and energy, etc.
· Vector: described by a magnitude and a direction. Example: force, displacement, velocity, acceleration, electric field and magnetic field, etc.
Vectors—Figures 1.9–1.10
· Vectors show magnitude and direction, drawn as a ray
|
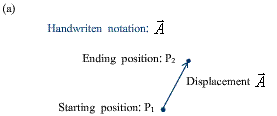 |
In print, we usually omit the arrow and just use a boldface letter to indicate a vector A.
The magnitude of a vector A is represented by the same letter in the light type A or |A| .
It is positive. |
 |
  |
|
Vector addition—Figures 1.11–1.12 |
· Vectors may be added graphically, “head to tail.”? |
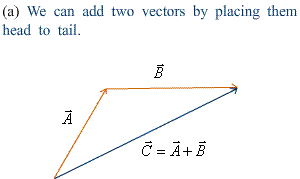 |
The sum or resultant (和)of two vectors. |
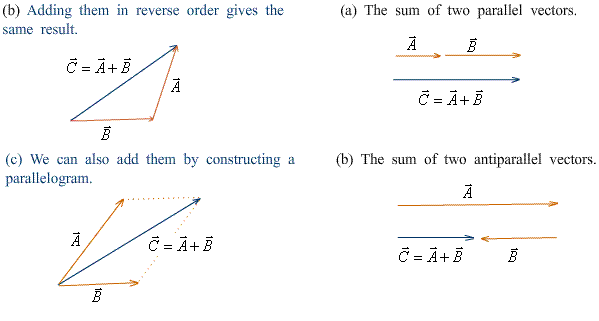 |
| |
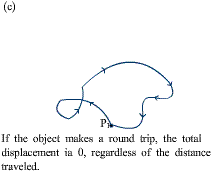
Vector addition—Figure 1.13 |
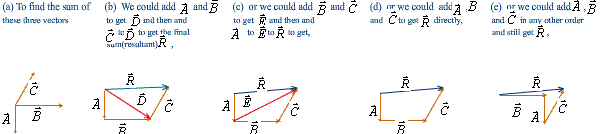 |
Commutative Law (交换律): A+B=B+A |
Associative Law (结合律): (A+B)+C=A+(B+C) |
|
Distributive Law (分配律):k(A+B)=kA+kB |
| |
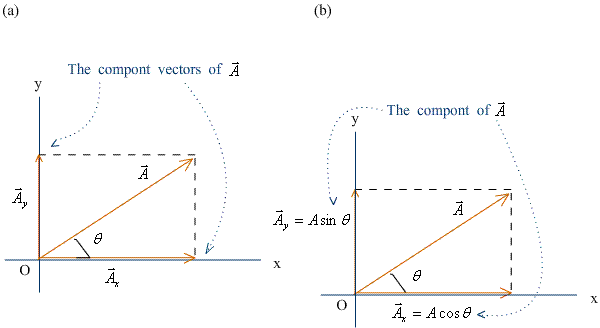
Components of vectors—Figure 1.17 |
· Manipulating vectors graphically is insightful but difficult when striving for numeric accuracy.? Vector components provide a numeric method of representation. |
· Any vector is built from an x component and a y component. |
|
 |
| |
Components of vectors II—Figure 1.18 |
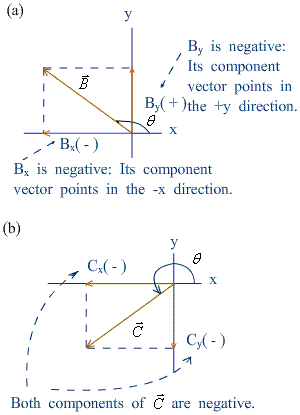 |
The component is just a number.
It can be positive or negative.
A vector can be obtained by the addition of its component vectors.
|
|
|
