|
Calculation using components—Figures 1.20–1.21
|
Vector sum calculated by using components
|
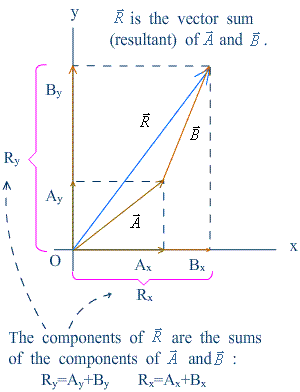 |
Find the right quadrant (象限) according to the sign of the components:
| |
I |
II |
III |
IV |
| x |
+ |
- |
- |
+ |
| y |
+ |
+ |
- |
- |
|
|
| |
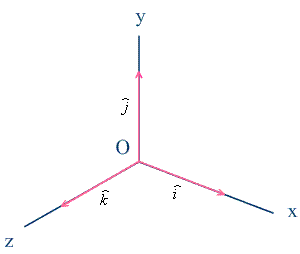
Unit vectors—Figures 1.23–1.24 |
· Unit vectors are vectors of unit length.
· The x direction is termed i, the y direction is termed j, and the z direction, k.
· A vector is subsequently described by a scalar? component times the corresponding unit vectors.?
|
 |
|
|
| |
Calculation using components in 3D |
|
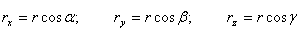 |
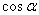 , , 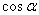 and and 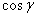 are direction cosines . are direction cosines . |
If  and and  |
We have 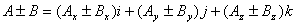 |
| |
Scalar product—Figures 1.25–1.26 |
· Termed the “dot product.” |
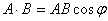 |
|
|
|
| |
Scalar product—Properties |
 |
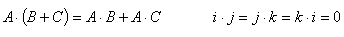 |
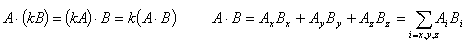 |
Example:? Let N to be a vector normal to the plane under consideration, which is drawn from an origin O in that plane.? Find out an equation to describe that plane.
|
|
| |
Scalar product |
Example:? Let N to be a vector normal to the plane under consideration, which is drawn from an origin O not in the plane.? Find out an equation to describe that plane.
|
|
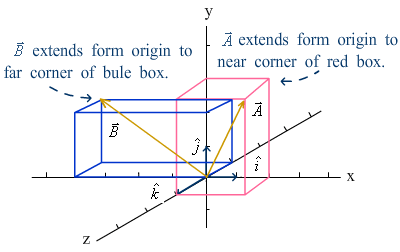 |
Find angle between two known vectors:
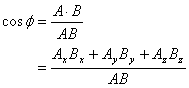
|
|
| |
Vector product—Figures 1.29–1.30 |
· Termed the “cross product.”
|
|
|
| |
Vector product—Basic properties |
 |
 |
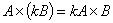 |
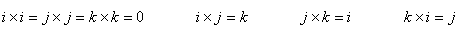 |
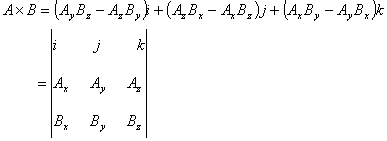 |
| |
Vector product—application |
|
area of a parallelogram (平行四边形) 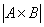 |
volume of a parallelepiped (平行六面体) 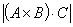 |
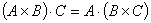 |
| |
|
