|
| |
Solving problems in physics
|
· Identify, set up, execute, evaluate
|
| |
Standards and units |
· Base units are set for length, time, and mass. |
· Unit prefixes size the unit to fit the situation.
|
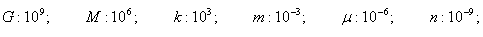 |
| |
Unit consistency and conversions |
· An equation must be dimensionally consistent (be sure you¡¯re ¡°adding apples to apples¡±).
|
· ¡°Have no naked numbers¡± (always use units in calculations). |
· Refer to Example 1.1 (page 7) and Problem 1.2 (page 8).
|
| |
Uncertainty and significant figures¡ªFigure 1.7 |
· Operations on data must preserve the data¡¯s accuracy.
|
· For multiplication and division, round to the smallest number of significant figures.
|
· For addition and subtraction, round to the least accurate data.
|
· Refer to Table 1.1, Figure 1.8, and Example 1.3.
|
· Errors can result in your rails ending in the wrong place. |
| |
Estimates and orders of magnitude |
· Estimation of an answer is often done by rounding any data used in a calculation.
|
· Comparison of an estimate to an actual calculation can ¡°head off¡± errors in final results. |
|
Example: |
A friend asks to borrow your precious diamond for a day to show her family. You are a bit worried, so you carefully have your diamond weighed on a scale which reads 8.17 grams. The scale¡¯s accuracy is claimed to be ¡À0.05 grams. The next day you weigh the returned diamond again, getting 8.09 grams. Is this your diamond?
|
|
