|
| |
Work and energy along a curved path
|
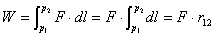 |
Work done by gravitational force: 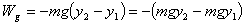 |
Gravitational potential energy (ÊÆÄÜ): 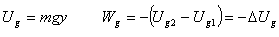 |
|
| |
Conservation of mechanical energy (»úеÄÜÊغã) |
If only gravitational force does work, according to the work-energy theorem, we have, |
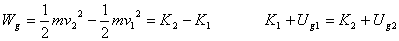 |
Mechanical energy: 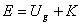 |
When only the force of gravity does work, the total mechanical energy of the system is conserved.
|
When forces other than gravity do work:
|
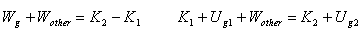 |
| |
Consider projectile motion using energetics |
· Consider the speed of a projectile as it traverses its parabola in the absence of air resistance.
|
· Refer to Conceptual Example 7.3 and Figure 7.8.
|
|
| |
What¡¯s the speed in a vertical circle? |
· Refer to Example 7.4 and Figure 7.9.
|
|
| |
Speed in a vertical circle with friction |
· Consider how things change when friction is introduced.
|
· Refer to Example 7.5 and Figure 7.10. |
|
| |
Work and energy in the motion of a mass on a spring |
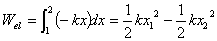 |
Elastic potential energy: 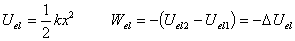 |
If only the elastic force does work: 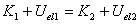 |
The mechanical energy is again conserved. |
|
| |
With both gravitational and elastic potential energy |
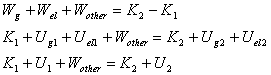 |
The work done by all forces other than the gravitational force or elastic force equals the change in the total mechanical energy E=K+U of the system.
|
|
