|
|
Entropy: a quantitative measure of disorder
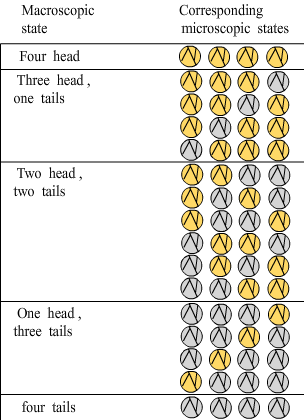
Macroscopic (ºê¹Û) state
Microscopic (΢¹Û) state
For any system, the most probable macroscopic state is the one with the greatest number of corresponding microscopic states, which is also the macroscopic state with the greatest disorder and the greatest entropy.
Entropy is a state function.
We are more interested in the change of entropy than the entropy itself.
|
 |
|
| |
Statistical view of entropy |
Phase space (Ïà¿Õ¼ä): The whole phase space can be divided into cells with a volume of 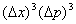 , where 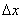 and 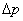 are uncertainties of the position and momentum. |
The microscopic state of a particle is represented by a point in the phase space. The distribution of the N particles among the cells in the phase space determines the bulk state.
|
The number of distributions that give rise to a macroscopic state the thermodynamic probability 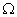 of that state. The states with the largest 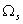 will be the ones most likely to occur. |
The entropy S is an extensive quantity. The entropy of two separate systems is 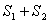 . The thermodynamic probability for two systems is 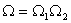 . |
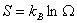 satisfies these properties. This is the Boltzman relation and satisfies these properties. This is the Boltzman relation and 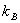 is the Boltzman constant. is the Boltzman constant. |
| |
Entropy change in a free expansion |
Suppose the number of microscopic states corresponding to an equilibrium state with volume V is 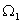 .
|
When the volume is doubled, each particle has twice as many possible states as compared to the previous ones.
|
|
| |
Entropy change |
Entropy change in an infinitesimal reversible process is 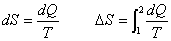 |
In a reversible isothermal process: 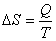 |
The total entropy change in one cycle of a Carnot engine is 0. 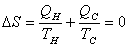 |
For any process between 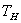 and 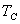 , 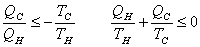 |
Clausius inequality for a cyclic process: 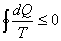
|
For a reversible cycle: 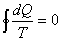 |
| |
Entropy change in irreversible processes |
| |
|
For any cyclic process:
For infinitesimal process: 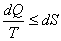 For an isolated system: 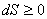 For a finite process: 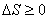 |
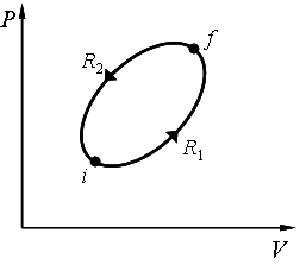 |
|
Second law of thermodynamics (principle of increasing entropy): the entropy of an isolated system never decreases.
|
| |
Entropy change of an ideal gas |
Suppose an ideal gas changes its state reversibly from 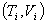 to 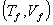 ,
|
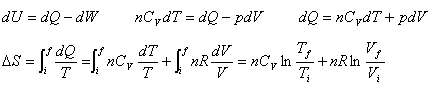 |
In a free expansion:
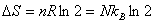 |
|
|